Ncert Exercises & Solutions

4.32. A particle falling vertically from a height hits a plane surface inclined to horizontal at an angle θ with speed $v_{0}$ $v_{0}$ and rebounds elastically. Find the distance along the plane where it will hit the second time.

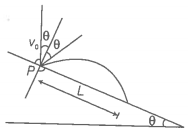
Hint: Time taken to travel the distances along OX and perpendicular to OX will be the same.

Step 1: For the motion of the projectile from O to A.

Considering x and y-axes as shown in the diagram.
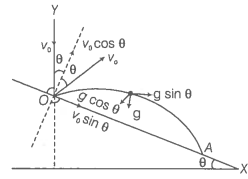
$\begin{array}{l} y = 0, u_{y} = v_{0} \cos θ \\ a_{y} = - g \cos θ, t = T \end{array}$

Applying the equation of kinematics

$\begin{matrix} y = u_{y} t + \frac{1}{2} a_{y} t^{2} \\ \Rightarrow 0 = v_{0} \cos θT + \frac{1}{2} (- gcos θ) T^{2} \\ \Rightarrow T [v_{0} \cos θ - \frac{gcos θ, T}{2}] = 0 \\ T = \frac{2 v_{0} \cos θ}{gcos θ} \end{matrix}$

Hence, $T = \frac{2 v_{0}}{g}$

Step 2: Now considering motion along OX.
$x = L, u_{x} = v_{0} \sin θ, a_{x} = gsin θ, t = T = \frac{2 v_{0}}{g}$
Applying the equation of kinematics,

$\begin{array}{l} x = u_{x} t + \frac{1}{2} a_{x} t^{2} \\ \Rightarrow L = v_{0} \sin θt + \frac{1}{2} gsin {θt}^{2} = (v_{0} \sin θ) (T) + \frac{1}{2} gsin {θT}^{2} \\ = (v_{0} \sin θ) (\frac{2 v_{0}}{g}) + \frac{1}{2} gsin θ \times (\frac{2 v_{0}}{g})^{2} \\ = \frac{2 v_{0}^{2}}{g} \sin θ + \frac{1}{2} gsin θ \times \frac{4 v_{0}^{2}}{g^{2}} = \frac{2 v_{0}^{2}}{g} [\sin θ + \sin θ] \\ \Rightarrow L = \frac{4 v_{0}^{2}}{g} \sin θ \end{array}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions