Please be patient as the PDF generation may take upto a minute.

1.

A straight section PQ of a circuit lies along the X-axis from x=$\frac{-\mathrm{a}}{2}$ to x= $\frac{\mathrm{a}}{2}$ and carries a steady current i. The magnetic field due to the section PQ at a point X = + a will be:
1. Proportional to a             2. Proportional to $a^2$
3. Proportional to $\frac{1}{a}$           4. Zero

2.

A circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r >> R, varies as 
1. $\frac{1}{r}$                                          
2. $\frac{1}{r^{3/2}}$
3. $\frac{1}{r^2}$                                          
4. $\frac{1}{r^3}$ 

3.

In the figure shown, the magnetic induction at the centre of the arc due to the current in portion AB will be

1. $\frac{{\mathrm{\mu }}_0\mathrm{i}}{\mathrm{r}}$                       3.  $\frac{{\mathrm{\mu }}_0\mathrm{i}}{4\mathrm{r}}$
2. $\frac{{\mathrm{\mu }}_0\mathrm{i}}{2\mathrm{r}}$                       4. Zero

4.

In the figure shown below there are two semicircles of radius \(r_1\) and \(r_2\) in which a current \(i\) is flowing. The magnetic induction at the centre of \(O\) will be:

 

1.	\(\dfrac{\mu_{0} i}{r} \left(r_{1} + r_{2}\right)\)	2.	\(\dfrac{\mu_{0} i}{4} \left[\frac{r_{1} + r_{2}}{r_{1} r_{2}}\right]\)
3.	\(\dfrac{\mu_{0} i}{4} \left(r_{1} - r_{2}\right)\)	4.	\(\dfrac{\mu_{0} i}{4} \left[\frac{r_{2} - r_{1}}{r_{1} r_{2}}\right]\)

5.

 The magnetic field at the centre of a coil of n turns, bent in the form of a square of side 2 l, carrying current i, is :
1.  $\frac{\sqrt{2}{\mathrm{\mu }}_0\mathrm{ni}}{\mathrm{\pi l}}$                               2.  $\frac{\sqrt{2}{\mathrm{\mu }}_0\mathrm{ni}}{2\mathrm{\pi l}}$
3.  $\frac{\sqrt{2}{\mathrm{\mu }}_0\mathrm{ni}}{4\mathrm{\pi l}}$                               4.  $\frac{2{\mathrm{\mu }}_0\mathrm{ni}}{\mathrm{\pi l}}$

6.

A and B are two concentric circular conductors of centre O and carrying currents ${\mathrm{i}}_{1 }$and ${\mathrm{i}}_2$ as shown in the adjacent figure. If ratio of their radii is 1 : 2 and ratio of the flux densities at O due to A and B is 1 : 3, then the value of ${\mathrm{i}}_1/{\mathrm{i}}_2$ is
 
1.  $\frac{1}{6}$                       2.  $\frac{1}{4}$                                
3.  $\frac{1}{3}$                       4.  $\frac{1}{2}$                                                                                                          

7.

A small coil of N turns has an effective area A and carries a current I. It is suspended in a horizontal magnetic field $\stackrel{.}{B}$ such that its plane is perpendicular to $\stackrel{.}{B}$. The work done in rotating it by $180°$ about the vertical axis is 
1. $NAIB$                               2. $2NAIB$ 
3. $2\mathrm{\pi NAIB}$                           4. $4\mathrm{\pi }NAIB$

8.

The magnetic field at the centre of a circular coil of radius r is $\mathrm{\pi }$ times that due to a long straight wire at a distance r from it, for equal currents. Figure here shows three cases : in all cases the circular part has radius r and straight ones are infinitely long. For same current the B field at the centre P in cases 1, 2, 3 have the ratio

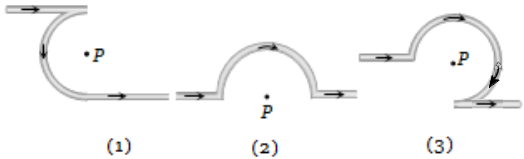
1. $\left(\frac{-\mathrm{\pi }}{2}\right)\mathbf{:}\left(\frac{\mathrm{\pi }}{2}\right)\mathbf{ }\mathbf{:}\left(\frac{3\mathrm{\pi }}{4}-\frac{1}{2}\right)$
2. $\left(-\frac{\mathrm{\pi }}{2}+1\right)\mathbf{:}\left(\frac{\mathrm{\pi }}{2}+1\right)\mathbf{:}\left(\frac{3\mathrm{\pi }}{4}+\frac{1}{2}\right)$
3. $-\frac{\mathrm{\pi }}{2}\mathbf{:}\frac{\mathrm{\pi }}{2}\mathbf{:}3\frac{\mathrm{\pi }}{4}$
4. $\left(-\frac{\mathrm{\pi }}{2}-1\right)\mathbf{:}\left(\frac{\mathrm{\pi }}{2}-\frac{1}{4}\right)\mathbf{:}\left(\frac{3\mathrm{\pi }}{4}+\frac{1}{2}\right)$

9.

A cell is connected between the points A and C of a circular conductor ABCD of centre O with angle AOC = $60°$ . If ${\mathrm{B}}_1$ and ${\mathrm{B}}_2$ are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio $\frac{{\mathrm{B}}_1}{{\mathrm{B}}_2}$ is:

1. 0.2                             
2. 6                                    
3. 1
4. 5                    

10.

 A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic field vector $\overrightarrow{\mathrm{B}}$ at a point having coordinates (x, y) in the z = 0 plane is :
1. $\frac{{\mathrm{\mu }}_0\mathrm{I}(\mathrm{y}\hat{\mathrm{i}}-\mathrm{x}\hat{\mathrm{j}})}{2\mathrm{\pi }({\mathrm{x}}^2+{\mathrm{y}}^2)}$                 
2. $\frac{{\mathrm{\mu }}_0\mathrm{I}(\mathrm{x}\hat{\mathrm{i}}+\mathrm{y}\hat{\mathrm{j}})}{2\mathrm{\pi }({\mathrm{x}}^2+{\mathrm{y}}^2)}$
3. $\frac{{\mathrm{\mu }}_0\mathrm{I}(\mathrm{x}\hat{\mathrm{j}}-\mathrm{y}\hat{\mathrm{i}})}{2\mathrm{\pi }({\mathrm{x}}^2+{\mathrm{y}}^2)}$                 
4. $\frac{{\mathrm{\mu }}_0\mathrm{I}(\mathrm{x}\hat{\mathrm{i}}-\mathrm{y}\hat{\mathrm{j}})}{2\mathrm{\pi }({\mathrm{x}}^2+{\mathrm{y}}^2)}$

11. A circular coil is in the \(y\text-z\) plane with its centre at the origin. The coil carries a constant current. Assuming the direction of the magnetic field at \(x= -25~\text{cm}\) to be positive, which of the following graphs shows the variation of the magnetic field along the \(x\text-\)axis?

1.		2.
3.		4.

12.

A particle with charge \(q\), moving with a momentum \(p\), enters a uniform magnetic field normally. The magnetic field has magnitude \(B\) and is confined to a region of width \(d\), where \(d< \frac{p}{Bq}.\) The particle is deflected by an angle \(\theta\) in crossing the field, then:
   

1.	\(\sin \theta=\frac{Bqd}{p}\)	2.	\(\sin \theta=\frac{p}{Bqd}\)
3.	\(\sin \theta=\frac{Bp}{qd}\)	4.	\(\sin \theta=\frac{pd}{Bq}\)

13.

A current-carrying loop is placed in a uniform magnetic field in four different orientations, I, II, III & IV. The decreasing order of potential energy is:

1.	I > III > II > IV	2.	I > II >III > IV
3.	I > IV > II > III	4.	III > IV > I > II

 

14.

The relation between voltage sensitivity (${\sigma }_v$) and current sensitivity (${\sigma }_i$) of a moving coil galvanometer is (Resistance of Galvanometer = G) 
1. $\frac{{\sigma }_i}{G}={\sigma }_v$                           
2. $\frac{{\sigma }_v}{G}={\sigma }_i$
3. $\frac{G}{{\sigma }_v}={\sigma }_i$                           
4. $\frac{G}{{\sigma }_i}={\sigma }_v$

15. A long straight wire of radius \(a\) carries a steady current \(I\). The current is uniformly distributed over its cross-section. The ratio of the magnetic fields \(B\) and \(B'\) at radial distances \(\frac{a}{2}\) and \(2a\) respectively, from the axis of the wire, is:

1.	\(\frac{1}{2}\)	2.	\(1\)
3.	\(4\)	4.	\(\frac{1}{4}\)