Please be patient as the PDF generation may take upto a minute.

A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to ${\mathrm{F}}_1$ on a particle placed at P, distance 2 R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the share as shown in figure. The sphere with cavity now applies a gravitational force ${\mathrm{F}}_2$ on same particle placed at P. The ratio ${\mathrm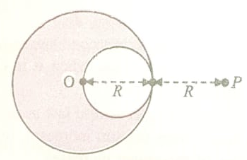{F}}_2/{\mathrm{F}}_1$ will be:

1. 1/2
2. 7/9
3. 3
4. 7

If a body is released from a point at a height equals to n times the radius of the earth R, its velocity equals reaching the surface of the earth is:
1. $\sqrt{\frac{ng R}{n+1}}$
2. $\sqrt{\frac{2ng R}{(n+1)}}$
3. $\sqrt{\frac{ng R}{2(n+1)}}$
4. $\sqrt{\frac{(n+1)g R}{2n}}$

The earth moves around the sun is an eclipse orbit as shown in the figure. The ratio $\frac{\mathrm{OA}}{\mathrm{OB}}=x\text{'}$. The ratio of the speed of the earth at B and at A is:

1. $\sqrt{x}$
2. x
3. ${\mathrm{x}}^2$
4. $x\sqrt{x}$

Two particle of equal mass go round a circle of radius R the action of their mutual gravitational attraction. The speed of each particle is:
1. V=$\sqrt{\frac{Gm}{2R}}$
2. V=$\frac{1}{2R}\sqrt{\frac{1}{Gm}}$
3. V=$\frac{1}{2}\sqrt{\frac{Gm}{R}}$
4. V=$\sqrt{\frac{4 Gm}{R}}$

What should be the speed with which the earth have rotate n ts axis s that a person n the equator would weighs (3/5)th as much as present? Given equational radius is R.
1. $\sqrt{2g/5R}$
2. $\sqrt{2R/\left(5g\right)}$
3. $2\sqrt{R}/\left(5\sqrt{g}\right)$
4. 2g/5R

A cube is subject to a uniform volume compression. If the side of the cube decreases by 1%, the bulk strain is:
1. 0.01
2. 0.02
3. 0.03
4. 0.06

A uniform rod of length L has a mass per unit length $\mathrm{\lambda }$ and area of cross-section A. The elongation in the rod is l due to its own weight if it is suspended from the ceiling if a room. The Young's modulus of the rod is:
1. $\frac{2\mathrm{\lambda } \mathrm{g} \mathrm{L}}{\mathrm{Al}}$
2. $\frac{\mathrm{\lambda } \mathrm{g} {\mathrm{L}}^2}{\mathrm{AL}}$
3. $\frac{\mathrm{\lambda } \mathrm{g} {\mathrm{L}}^2}{2\mathrm{Al}}$
4. $\frac{2\mathrm{\lambda } \mathrm{g} {\mathrm{L}}^2}{\mathrm{Al}}$

Two equal masses m and m are hung from a balance whose scale pan differs in vertical height by h/2. The error in weighing in terms of density of the earth $\mathrm{\rho }$ is:
1. $\frac{1}{3}\mathrm{\pi } \mathrm{G} \mathrm{\rho } \mathrm{mh}$
2. $\mathrm{\pi } \mathrm{G} \mathrm{\rho } \mathrm{mh}$
3. $\frac{4}{3}\mathrm{\pi } \mathrm{G} \mathrm{\rho } \mathrm{mh}$
4. $\frac{8}{3} \mathrm{G} \mathrm{\rho } \mathrm{mh}$

A straight rod of L extends from x=a to x=L+a. The gravitational force it exerts on a point mass m at x=0 if the mass per unit length is $\mathrm{A}+\mathrm{B} {\mathrm{x}}^2$ is:
1. $Gm\left[A\left(\frac{1}{a+1}-\frac{1}{a}\right)+BL\right]$
2. $Gm\left[A\left(\frac{1}{a}-\frac{1}{a\mathit{+}\mathit{1}}\right)+BL\right]$
3. $Gm\left[A\left(\frac{1}{a+1}-\frac{1}{a}\right)\mathit{-}BL\right]$
4. $Gm\left[A\left(\frac{1}{a}-\frac{1}{\mathit{(}a\mathit{+}\mathit{1}\mathit{)}}\right)\mathit{-}BL\right]$

The minimum and maximum distances of  a staellite from the centre of the earth are 2 R and 4 R respectively, where R is the radius of the earth and M is the mass of earth. The radius of curvature of the satellite orbit of the point of maximum distance is:
1. $\frac{2R}{3}$
2. $\frac{4R}{3}$
3. $\frac{8 R}{3}$
4. $\frac{16 R}{3}$

One end of a uniform rod of mass ${\mathrm{m}}_1$, uniform area of cross-section A is suspended from the roof and a mass ${\mathrm{m}}_2$ is suspended from the other end. What is the stress at the mid point of the rod?
1. $({\mathrm{m}}_1+{\mathrm{m}}_2) \mathrm{g}/\mathrm{A}$
2. $({\mathrm{m}}_1-{\mathrm{m}}_2) \mathrm{g}/\mathrm{A}$
3. $\left[\frac{({\mathrm{m}}_1/2)+{\mathrm{m}}_2}{\mathrm{A}}\right]g$
4. $\left[\frac{{\mathrm{m}}_1+({\mathrm{m}}_2/2)}{\mathrm{A}}\right]g$
$$

Two wires of equal length and cross-section area suspended as shown in Figure. Thier Young's modulus are ${\mathrm{Y}}_1 \mathrm{and} {\mathrm{Y}}_2$ respectively. The equivalent Young's modulus will be:

1. ${\mathrm{Y}}_1+{\mathrm{Y}}_2$
2. $\frac{{\mathrm{Y}}_1+{\mathrm{Y}}_2}{2}$
3. $\frac{{\mathrm{Y}}_1{\mathrm{Y}}_2}{{\mathrm{Y}}_1+{\mathrm{Y}}_2}$
4. $\sqrt{Y_1{Y}_2}$

If the ratio of lengths, radii and Young's modulii of steel and brass wires in the figure are a, b, c respectively. Then the corresponding ratio of increase in their length would be:

1. $\frac{2ac}{b^2}$
2. $\frac{3a}{2b^{2}c}$
3. $\frac{3c}{2a{b}^2}$
4. $\frac{2a^{2}c}{b}$

Two cylinders A and B of radii r and 2 r are soldered co-axially. The free end of A is clamped and free end of B is twisted by an angle $\mathrm{\varphi }$. The twist at the junction, taking the material of two cylinders to be same and length equal, is:
1. $\frac{15}{16}\varphi$
2. $\frac{16}{17}\varphi$
3. $\frac{16}{15}\varphi$
4. $\frac{17}{16}\varphi$

Two equal and opposite force F and -F act on a rod os uniform cross-sectional area A as shown in Figure. The longitudinal stress on the section AB is:

1. $\frac{F}{A}$
2. $\frac{2F}{A}$
3. $\frac{F}{A} \sin \theta$
4. $\frac{F}{A} {\sin }^2\theta$

A thin uniform metallic rod of length L and area of cross-section A rotates with an angular velocity $\mathrm{\omega }$ in a horizontal plane about a vertical axis passing through one of its ends. If $\mathrm{\rho }$ is the density of the rod, the maximum tension in the rod is:
1. $\frac{1}{2}\rho A {\omega }^2{L}^2$
2. $\frac{1}{2}\rho A {\omega }^{2}L$
3. $\frac{1}{3}\rho A {\omega }^2{L}^2$
4. $\frac{1}{3}\rho A {\omega }^{2}L$

A steel rod of length l, area of cross-section A, Young's Modulus Y and linear coefficient of expansion $\mathrm{\alpha }$ is heated through ${\mathrm{t}}^2\mathrm{C}$. the work that can be performed by the rod when heated is:
1. $\frac{1}{2}(YA \alpha t)\times (l \alpha t)$
2. $(\mathrm{YA} \mathrm{\alpha } \mathrm{t})\times \left(\mathrm{t} \mathrm{\alpha } \mathrm{t}\right)$
3. $2(\mathrm{YA} \mathrm{\alpha } \mathrm{t})\times (\mathrm{l} \mathrm{\alpha } \mathrm{t})$
4. $\frac{1}{2}(YA \alpha t)\times \left(\frac{1}{2}l \alpha t\right)$

A wire of cross-sectional area A is stretched horizontally between two clamps located at a  distance l metres from each other. A weight W kg is suspended from the mid point of the wire. If the verticle distance through which the mid point of the wire moves down be x<l, then the strain produced in the wire is:
1. ${\mathrm{x}}^2/(4 {\mathrm{l}}^2)$
2. ${\mathrm{x}}^2/(2 {\mathrm{l}}^2)$
3. ${\mathrm{x}}^2/{\mathrm{l}}^2$
4. $2 {\mathrm{x}}^2/{\mathrm{l}}^2$

A constant force ${\mathrm{F}}_0$ is applied on a uniform elastic strig placed over a smooth horizontal surface as shown in Figure. Young's modulus of string is Y and area of cross-section is A. The strain produced in the string in the direction of force is:

1. $\frac{F_{0}Y}{A}$
2. $\frac{F_0}{AY}$
3. $\frac{F_0}{2 AY}$
4. $\frac{F_{0}Y}{2A}$

A steel ring of radius r and cross-section area A is fitted on to a wooden disc of radius R (R>r). If Young's modulus be Y, then the force with which the steel ring is expanded, is:
1. $AY\frac{R}{r}$
2. $AY\left[\frac{R-r}{r}\right]$
3. $\frac{Y}{A}\left[\frac{R-r}{r}\right]$
4. $\frac{Y r}{AR}$