Please be patient as the PDF generation may take upto a minute.

The deformation of a wire under its own weight compared to the deformation of the same wire subjected a tension equal to the weight of the wire is
1.  same
2.  one third
3.  half
4.  one fourth 

The stress-strain graph for two materials is shown in the figure. If the Young's modulus for two materials are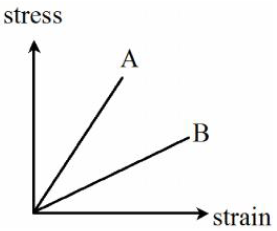 $Y_A$ and $Y_B$, then-

(1) $Y_A$ = $Y_B$
(2) $Y_A$ > $Y_B$
(3) $Y_A$ < $Y_B$
(4) Can't be predicted from the graph 

A wire of length L, cross-sectional area A is made of a material of Young's modulus Y.
The wire is stretched by an amount x, by a constant force which lies well within the
elastic limit. The work done (W) by the force is 
1. $W=\frac{Y{x}^2}{L^2}$
2. $W=\frac{Y{x}^2}{2L^2}$
3. $W=\frac{1}{2} \frac{YA{x}^2}{L}$
4.$W=\frac{YA{x}^2}{L}$

lf \(\rho\) is the density of the material of a wire and \(\sigma\) is the breaking stress, the greatest length of the wire that can hang freely without breaking is:
1. \(\dfrac{2}{\rho g}\)
2. \(\dfrac{\rho}{\sigma g}\)
3. \(\dfrac{\rho g}{2 \sigma}\)
4. \(\dfrac{\sigma}{\rho g}\)

An elastic material of Young's modulus \(Y\) is subjected to a stress \(S\). The elastic energy stored per unit volume of the material is:
1. \(\frac{SY}{2}\)
2. \(\frac{S^2}{2Y}\)
3. \(\frac{S}{2Y}\)
4. \(\frac{2S}{Y}\)

The following four wires are made of the same material. Which of these will have the largest extension, when the same tension is applied?
1.  length 50 cm and diameter 0.5 mm
2.  length 100 cm and diameter 1 mm
3.  length 200 cm and diameter 2 mm
4.  length 300 cm and diameter 3 mm

Two wires A and B are of the same material. Their lengths are in the ratio 1 : 2 and the diameters are in the ratio 2 : 1. If they are pulled by the same force, their increase in length will be in the ratio
1.  2 : 1
2.  1 : 4
3.  1 : 8
4.  8 : 1 

A material has Poisson's ratio of \(0.5\). If a uniform rod made of it suffers a longitudinal strain of \(2\times 10^{-3}\), what is the percentage increase in volume?
1. \(2\%\)
2. \(4\%\)
3. \(0\%\)
4. \(5\%\)

One end of a long metallic rod of length L is tied to the ceilling. The other end is tied to
massless spring of spring constant k. A mass m hangs freely from the free end of the
spring. The area of cross-section and Young's modulus of the wire  A and y
respectively. lf the mass is slightly pulled down and released. lf the mass is slightly
pulled down and released . it will oscillate with a time period T equal to 
1. $2\mathrm{\pi }\sqrt{\left(\frac{\mathrm{m}}{\mathrm{k}}\right)}$
2. $2\mathrm{\pi }{\left[\frac{(\mathrm{YA} + \mathrm{kL})\mathrm{m}}{\left(\mathrm{YAk}\right)}\right]}^{1/2}$
3. $2\mathrm{\pi }\sqrt{\left(\frac{\mathrm{mYA}}{\mathrm{kL}}\right)}$
4. $2\mathrm{\pi }\sqrt{\left(\frac{\mathrm{mL}}{\mathrm{YA}}\right)}$

If the ratio of lengths, radii, and Young's modulus of steel and brass wires in the figure are \(a,\) \(b\) and \(c\) respectively, then the corresponding ratio of increase in their lengths will be:
                                 
1. \(\dfrac{2 a^{2} c}{b}\)
2. \(\dfrac{3 a}{2 b^{2} c}\)
3. \(\dfrac{2 a c}{b^{2}}\)
4. \(\dfrac{3 c}{2 a b^{2}}\)

The density of metal at normal pressure is \(\rho\)$\mathrm{}$. lts density when it is subjected to an excess pressure \(P\) is \(\rho'\). lf \(B\) is the bulk modulus of the metal, the ratio \(\frac{ρ'}{\rho }\) is:
1. \(\frac{1}{1-\frac{p}{B}} \)
2. \(1+\frac{B}{P} \)
3. \(\frac{1}{1-\frac{B}{P}} \)
4. \(2+\frac{P}{B}\)

A uniform cylinder rod of length \(L\), cross-sectional area \(A\) and Young's modulus \(Y\) is acted upon by the forces, as shown in the figure. The elongation of the rod is:
           
1. \(\frac{3FL}{5AY}\)
2. \(\frac{2FL}{5AY}\)
3. \(\frac{2FL}{8AY}\)
4. \(\frac{8FL}{3AY}\)

Two wires are made of the same material and have the same volume. However wire 1
has cross sectional area A and Wire 2 has cross-sectional area 3A. lf the length of wire
1 increases by $∆x$ on applying force F, how much forces is needed to stretch wire 2 by
the same amount 
1. F 
2. 4 F
3. 6 F
4. 9 F

A wire of lingth 2 L and radius r is stretched between A and B without the application
of any tension. If Y is the Young's modulus of the wire and it is stretched like ACB,
then the tension in the wire will be (Assume d<<) 
(1) $\frac{{\mathrm{\pi r}}^2{\mathrm{yd}}^3}{2L^2}$
(2) $\frac{{\mathrm{\pi r}}^2{\mathrm{yd}}^2}{2L^2}$
(3) $\frac{{\mathrm{\pi r}}^2\mathrm{Y}.2{\mathrm{L}}^2}{d^2}$
(4) $\frac{{\mathrm{\pi r}}^{2}Y.2L}{d}$
 
 

A wire of length L is hanging from a fixed support. The length changes to L₁ and L₂ when
masses M₁ and M₂ are suspended respectively from its free end. Then L is equal to-
1. $\frac{L_1+L_2}{2}$
2. $\sqrt{L_1{L}_2}$
3. $\frac{L_1{M}_{2 }+L_2{M}_1}{M_1+M_2}$
4. $\frac{L_1{M}_2-L_2{M}_1}{M_2-M_1}$

Two blocks of masses 1 kg  and 2 kg are suspended with the help of two wires having the same area of cross-section. It the ratio of Young's moduli i.e Y${}_1$ : Y${}_2$= 1:2, then the ratio of extensions produced in wires is: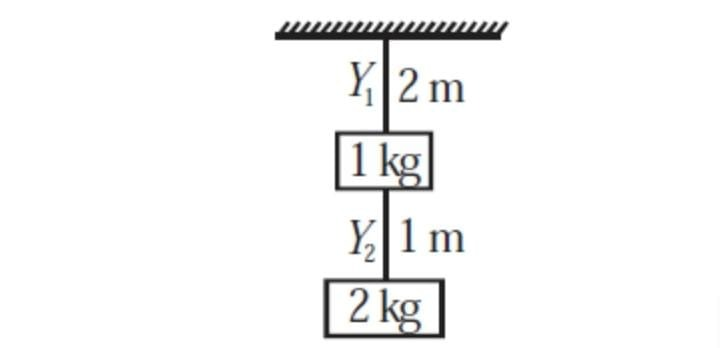

1. 2 : 1 
2. 4 : 1 
3. 6 : 1 
4. 8 : 1 

One end of a horizontal thick copper wire of length 2L and radius 2R is welded to an end
of another horizontal thin copper wire of length L and radius R. When the thin copper
wire of length L and radius R. When the arragement is stretched by a applying forces at
two ends, the ratio of the elongation in the thin wire to that in the thick wire is 
1. 025
2. 0.50 
3. 2.00 
4. 4.00 

A wire of length L and cross- sectional area A is made of a material of Young's modulus Y
It is stretched by an amout x, The energy stored is 
1. $\frac{YxA}{2L}$
2.$\frac{Y{x}^{2}A}{L} \mathbf{ }\mathbf{ }$
3. $\frac{Y{x}^{2}A}{2L}$
4.$\frac{2Y{x}^{2}A}{L}$

Glass is 
1. Ductile 
2. Malleable 
3. Britle 
4. Sonorous