Please be patient as the PDF generation may take upto a minute.

1.

A charged particle of mass 'm' having charge 'q' is moving in a circular path of radius 'R' in uniform magnetic field 'B'. The average force on the particle during the time it completes half the revolution is
1. $\frac{2{\mathrm{q}}^2{\mathrm{B}}^2\mathrm{R}}{\mathrm{\pi m}}$
2. $\frac{{\mathrm{q}}^2{\mathrm{B}}^2\mathrm{R}}{\mathrm{\pi m}}$
3. $\frac{{\mathrm{q}}^2{\mathrm{B}}^2\mathrm{R}}{2\mathrm{m}}$
4. $\frac{{\mathrm{q}}^2{\mathrm{B}}^2\mathrm{R}}{2\mathrm{\pi m}}$

2.

If a diamagnetic substance is brought near north or south pole of a bar magnet, it is :-
1. Attracted by the poles.
2. Repelled by the poles.
3. Repelled by the north pole and attracted by the south pole.
4. Attracted by the north pole and repelled by the south pole.

3.

Magnetic susceptibility of a di–magnetic substance varies with absolute temperature as :-
1. directly proportional to T.
2. inversely proportional to T.
3. remains unchanged with T.
4. exponential decrease with T.

4.

If the magnetic dipole moment of an atom of diamagnetic material, paramagnetic material and ferromagnetic material are denoted by ${\mu }_d, {\mu }_p and {\mu }_f$ , and respectively,
then :-
1. ${\mu }_p=0 and {\mu }_f\ne 0$
2. ${\mu }_d\ne 0 and {\mu }_p=0$
3. ${\mu }_d\ne 0 and {\mu }_f\ne 0$
4. ${\mu }_d=0 and {\mu }_p\ne 0$

5.

A flexible wire of length L forming a loop is placed in uniform magnetic field 'B'. When a current 'i' is set up in the loop it forms a circle. FInd the tension in the loop.
1. $\frac{\mathrm{BiL}}{2\mathrm{\pi }}$
2. $\frac{\mathrm{BiL}}{\mathrm{\pi }}$
3. BiL
4. $\frac{\mathrm{BiL}}{2}$

6.

The magnetic susceptibility of a paramagnetic substance is 3 × 10^–4. It is placed in a magnetising field of 4 × 10⁴ A/m. The intensity of magnetisation will be :-
1. 3 × 10⁸ A/m
2. 12 × 10⁸ A/m
3. 12 A/m
4. 24 A/m

7. If a wire in the form of a square with a side \(a\) carries a current \(i\), then the magnetic induction at the centre of the square wire will be:
(Magnetic permeability of free space = \(\mu_0)\)

1.	\(\dfrac{\mu _{0}i}{2\pi a}\)	2.	\(\dfrac{\mu _{0}i\sqrt2}{\pi a}\)
3.	\(\dfrac{2\sqrt2\mu _{0}i}{\pi a}\)	4.	\(\dfrac{\mu _{0}i}{\sqrt2\pi a}\)

 

8.

A proton and an \(\alpha\text-\)particle enter a uniform magnetic field perpendicularly at the same speed. If a proton takes \(25~\mu\text{s}\) to make \(5\) revolutions, then the periodic time for the \(\alpha\text-\)particle will be:
1. \(50~\mu\text{s}\)
2. \(25~\mu\text{s}\)
3. \(10~\mu\text{s}\)
4. \(5~\mu\text{s}\)

9.

The charge on a particle Y is double the charge on particle X. These two particles X and Y after being accelerated through the same potential difference enter a region of the uniform magnetic field and describe circular paths of radii $R_1$ and $R_2$ respectively. The ratio of the mass of X to that of Y is:
1. ${\left(\frac{2R_1}{R_2}\right)}^2$                     
2. ${\left(\frac{R_1}{2R_2}\right)}^2$
3.  $\frac{R_1^2}{2R_2^2}$                           
4. $\frac{2R_1}{R_2}$ 

10.

A cell is connected between the points A and C of a circular conductor ABCD of centre O with angle AOC = $60°$ . If ${\mathrm{B}}_1$ and ${\mathrm{B}}_2$ are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio $\frac{{\mathrm{B}}_1}{{\mathrm{B}}_2}$ is:

1. 0.2                             
2. 6                                    
3. 1
4. 5                    

11.

A current-carrying wire is placed in a uniform magnetic field in the shape of the curve \(y= \alpha \sin \left({\pi x \over L}\right),~0 \le x \le2L.\) $$
What will be the force acting on the wire?
               

1.	\(iBL \over \pi\)	2.	\(iBL \pi\)
3.	\(2iBL \)	4.	zero

12.

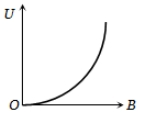
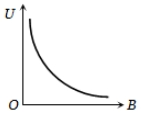
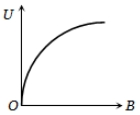
If induction of magnetic field at a point is B and energy density is U, then which of the following graphs is correct?
1. 
2. 
3. 
4. 

13.

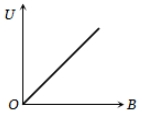
In the given figure net magnetic field at O will be  i

1. $\frac{{\mu }_{0}i}{3\mathrm{\pi a}}\sqrt{4-{\mathrm{\pi }}^2}$                                 
2. $\frac{{\mu }_{0}i}{3\mathrm{\pi a}}\sqrt{4+{\mathrm{\pi }}^2}$
3. $\frac{2{\mu }_{0}i}{3\mathrm{\pi a}}\sqrt{4+{\mathrm{\pi }}^2}$                                 
4. $\frac{2{\mu }_{0}i}{3\mathrm{\pi a}}\sqrt{\left(4-{\mathrm{\pi }}^2\right)}$

14.

A current-carrying loop is placed in a uniform magnetic field in four different orientations, I, II, III & IV. The decreasing order of potential energy is:

1.	I > III > II > IV	2.	I > II >III > IV
3.	I > IV > II > III	4.	III > IV > I > II

 

15. A long straight wire of radius \(a\) carries a steady current \(I\). The current is uniformly distributed over its cross-section. The ratio of the magnetic fields \(B\) and \(B'\) at radial distances \(\frac{a}{2}\) and \(2a\) respectively, from the axis of the wire, is:

1.	\(\frac{1}{2}\)	2.	\(1\)
3.	\(4\)	4.	\(\frac{1}{4}\)

16.

Two equal bar magnets are kept as shown in the figure. The direction of the resultant magnetic field, indicated by arrowhead at the point \(P\) is: (approximately)
          

1.		2.
3.		4.

17.

If the angles of dip at two places are 30^o and 45^o respectively, then the ratio of horizontal  components of earth's magnetic field at the two places will be:
(Assume net magnetic field to be equal at the two places)
1. √3 : √2
2. 1 : √2
3. 1 : √3
4. 1 : 2

18.

If a magnet is suspended at an angle 30^o to the magnetic meridian, it makes an angle of 45^o with the horizontal. The real dip is
1. ${\tan }^{-1}\left(\frac{\sqrt{3}}{2}\right)$
2. ${\tan }^{-1}\left(\sqrt{3}\right)$
3. ${\tan }^{-1}\left(\sqrt{\frac{3}{2}}\right)$
4. ${\tan }^{-1}\left(\frac{2}{\sqrt{3}}\right)$

19.

If at any place, the angle of dip is  $\theta$ and magnetic latitude is $\lambda$, then (assume that the axis of earth's magnetic moment coincides with axis of rotation of the earth)
1. $\theta$ =  $\lambda$
2. tan$\theta$ = cos$\lambda$
3. tan$\theta$.cot$\lambda$ = 2
4. tan$\theta$.cot$\lambda$ =$\frac{1}{2}$

20.

A bar magnet of length l and magnetic dipole moment M is bent to form an arc which subtends an angle of $120°$ at centre. The new magnetic dipole moment will be
1.  $\frac{3\mathrm{M}}{2\mathrm{\pi }}$
2.  $\frac{3\sqrt{3}\mathrm{M}}{2\mathrm{\pi }}$
3.  $\frac{3\mathrm{M}}{\mathrm{\pi }}$
4.  $\frac{2\mathrm{M}}{\mathrm{\pi }}$