Please be patient as the PDF generation may take upto a minute.

A ring of charge with radius 0.5 m has 0.002$\mathrm{\pi }$ m gap. If the ring carries a charge +1 C, the electric field at the centre is:
     
1. $7.5\times {10}^7 N{C}^{-1}$
2. $7.2\times {10}^7 N{C}^{-1}$
3. $6.2\times {10}^7 N{C}^{-1}$
4. $6.5\times {10}^7 N{C}^{-1}$

For an isolated charged conductor shown in Fig. the potential at points A, B, c and D are V${}_{\mathrm{A}}$, V${}_{\mathrm{B}}$, V${}_{\mathrm{C}}$, and V${}_{\mathrm{D}}$, respectively. Then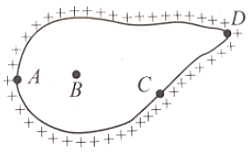

$1. {\mathrm{V}}_{\mathrm{A}} = {\mathrm{V}}_{\mathrm{B}}>{\mathrm{V}}_{\mathrm{C}}>{\mathrm{V}}_{\mathrm{D}}$
$2. {\mathrm{V}}_{\mathrm{D}}>{\mathrm{V}}_{\mathrm{C}}>{\mathrm{V}}_{\mathrm{B}} = {\mathrm{V}}_{\mathrm{A}}$
$3. {\mathrm{V}}_{\mathrm{D}}>{\mathrm{V}}_{\mathrm{C}}>{\mathrm{V}}_{\mathrm{B}}>{\mathrm{V}}_{\mathrm{A}}$
$4. {\mathrm{V}}_{\mathrm{D}} = {\mathrm{V}}_{\mathrm{C}} = {\mathrm{V}}_{\mathrm{B}} = {\mathrm{V}}_{\mathrm{A}}$

Three capacitors \(A\), \(B\) and \(C\) are connected in a circuit as shown in Fig. What is the charge in \(\mu \text{C}\) on the capacitor \(B\):
 

A particle of mass \(m\) and charge \(\text-q\) moves diametrically through a uniformly charged sphere of radius \(R\) with total charge \(Q\). The angular frequency of the particle's simple harmonic motion, if its amplitude \(<R\), is given by:
1. \(\sqrt{\dfrac{qQ}{4 \pi \varepsilon_0 ~mR} }\)
2. \(\sqrt{\dfrac{qQ}{4 \pi \varepsilon_0 ~mR^2} }\)
3. \(\sqrt{\dfrac{qQ}{4 \pi \varepsilon_0 ~mR^3}}\)
4. \( \sqrt{\dfrac{m}{4 \pi \varepsilon_0 ~qQ} }\)

In the circuit shown in Fig. C = 6 $\mathrm{\mu }$F. The charge stored in the capacitor of capacity C is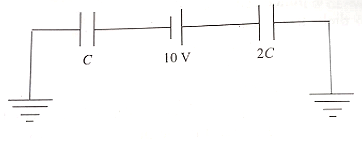

1. zero
2. 90 $\mathrm{\mu }$C
3. 40 $\mathrm{\mu }$C
4. 60 $\mathrm{\mu }$C
 

In Fig., if the potential at point B is taken as zero, then the potential at point A will be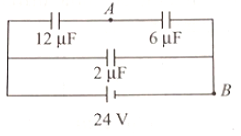

1. 8 V
2. 16 V
3. 24 V
4. none of the above

A charge +q is fixed at each of the points $\mathrm{x} = {\mathrm{x}}_0, \mathrm{x} = 3{\mathrm{x}}_0, \mathrm{x} = 5{\mathrm{x}}_0, ....$ upto $\infty$ on X-axis and charge -q is fixed on each of the points $\mathrm{x} = 2{\mathrm{x}}_0, \mathrm{x} = 4{\mathrm{x}}_0, \mathrm{x} = 6{\mathrm{x}}_0, ....$ upto $\infty$. Here ${\mathrm{x}}_0$ is a positive constant. Take the potential at a point due to a charge Q at a distance r from it to be  $\frac{\mathrm{Q}}{4{\mathrm{\pi \epsilon }}_0\mathrm{r}}$. Then the potential at the origin due to above system of charges will be
$1. \mathrm{zero}$
$2. \frac{\mathrm{q}}{8{\mathrm{\pi \epsilon }}_0{\mathrm{x}}_0{\log }_{\mathrm{e}}2}$
$3. \mathrm{infinity}$
$4. \frac{\mathrm{q} {\log }_{\mathrm{e}}2}{4{\mathrm{\pi \epsilon }}_0{\mathrm{x}}_0}$

Three concentric charged metallic spherical shells A, B and C have radii a, b and c; charge densities $\mathrm{\sigma }, -\mathrm{\sigma }$ and $\mathrm{\sigma }$ and potential ${\mathrm{V}}_{\mathrm{A}}, {\mathrm{V}}_{\mathrm{B}}$ and ${\mathrm{V}}_{\mathrm{C}}$ respectively. Then which of the following relations is correct?
$1. {\mathrm{V}}_{\mathrm{A}} = \left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\frac{\mathrm{\sigma }}{{\mathrm{\epsilon }}_0}$
$2. {\mathrm{V}}_{\mathrm{B}} = \left(\frac{{\mathrm{a}}^2}{\mathrm{b}}-\mathrm{b}+\mathrm{c}\right)\frac{\mathrm{\sigma }}{{\mathrm{\epsilon }}_0}$
$3. {\mathrm{V}}_{\mathrm{C}} = \left(\frac{{\mathrm{a}}^2+{\mathrm{b}}^2}{\mathrm{b}}+\mathrm{c}\right)\frac{\mathrm{\sigma }}{{\mathrm{\epsilon }}_0}$
$4. {\mathrm{V}}_{\mathrm{A}} = {\mathrm{V}}_{\mathrm{B}} = {\mathrm{V}}_{\mathrm{C}} = \left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\frac{\mathrm{\sigma }}{{\mathrm{\epsilon }}_0}$

Two parallel-plate capacitors of capacitances C and 2C are connected in parallel and charged to potential differences V. The battery is then disconnected and the region between the plates of C is filled completely with a material of dielectric constant K. The common potential difference across the combination becomes
$1. \frac{2\mathrm{V}}{\mathrm{K}+2}$
$2. \frac{\mathrm{V}}{\mathrm{K}+2}$
$3. \frac{3\mathrm{V}}{\mathrm{K}+3}$
$4. \frac{3\mathrm{V}}{\mathrm{K}+2}$

The electric potential at a point (x, y, z) is given by V = $-{\mathrm{x}}^2\mathrm{y}-{\mathrm{xz}}^3+4$. The electric field $\overrightarrow{\mathrm{E}}$ at that point is
$1. \overrightarrow{\mathrm{E}} = \hat{\mathrm{i}} 2\mathrm{xy}+\hat{\mathrm{j}}\left({\mathrm{x}}^2+{\mathrm{y}}^2\right)+\hat{\mathrm{k}}\left(3\mathrm{xz}-{\mathrm{y}}^2\right)$
$2. \overrightarrow{\mathrm{E}} = \hat{\mathrm{i}} {\mathrm{z}}^3+\hat{\mathrm{j}} \mathrm{xyz}+\hat{\mathrm{k}} {\mathrm{z}}^2$
$3. \overrightarrow{\mathrm{E}} = \hat{\mathrm{i}}\left(2\mathrm{xy}-{\mathrm{z}}^3\right)+\hat{\mathrm{j}} {\mathrm{xy}}^2+\hat{\mathrm{k}} 3{\mathrm{z}}^2\mathrm{x}$
$4. \overrightarrow{\mathrm{E}} = \hat{\mathrm{i}}\left(2\mathrm{xy}+{\mathrm{z}}^3\right)+\hat{\mathrm{j}} {\mathrm{x}}^2+\hat{\mathrm{k}} 3{\mathrm{xz}}^2$

Two point dipoles of dipole moment \(\vec{p}_{1}\) and \(\vec{p}_{2}\) are at a distance \(x\) from each other and \(\vec{p}_{1} \left|\right| \vec{p}_{2}\). The force between the dipole is:
1. \(\frac{1}{4 π\varepsilon_{0}} \frac{4 p_{1} p_{2}}{x^{4}}\)
2. \(\frac{1}{4 π\varepsilon_{0}} \frac{3 p_{1} p_{2}}{x^{3}}\)
3. \(\frac{1}{4π\varepsilon_{0}} \frac{6 p_{1} p_{2}}{x^{4}}\)
4. \(\frac{1}{4 π\varepsilon_{0}} \frac{8 p_{1} p_{2}}{x^{4}}\)

Consider an electric field $\overrightarrow{\mathrm{E}}=E_0\hat{x}$ where ${\mathrm{E}}_0$ is a constant. The flux through the shaded area(as shown in the figure) due to this field is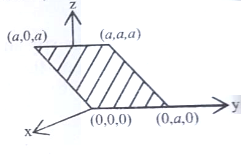 

1. $2E_0{a}^2$
2. $\sqrt{2}{E}_0{a}^2$
3. $E_0{a}^2$
4. $\frac{E_0{a}^2}{\sqrt{2}}$

Five identical plates each of area A are joined as shown in the figure. The distance between the plates is d. The plates are connected to a potential difference of V volt. The charge on plates 1 and 4 will be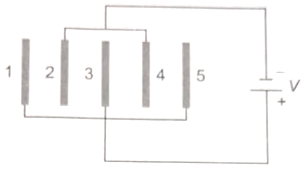

1. $-\frac{{\epsilon }_{0}AV}{d},\frac{2{\epsilon }_{0}AV}{d}$
2. $\frac{{\epsilon }_{0}AV}{d},\frac{2{\epsilon }_{0}AV}{d}$
3. $\frac{{\epsilon }_{0}AV}{d},\frac{-2{\epsilon }_{0}AV}{d}$
4. $-\frac{{\epsilon }_{0}AV}{d},\frac{-2{\epsilon }_{0}AV}{d}$

A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field E at the centre O is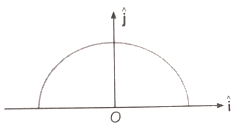 

1. $\frac{q}{4{\pi }^2{\epsilon }_0{\mathrm{r}}^2}\hat{j}$
2. $-\frac{q}{4{\pi }^2{\epsilon }_0{\mathrm{r}}^2}\hat{j}$
3. $-\frac{q}{2{\pi }^2{\epsilon }_0{\mathrm{r}}^2}\hat{j}$
4. $\frac{q}{2{\pi }^2{\epsilon }_0{\mathrm{r}}^2}\hat{j}$

Some equipotential surface are shown in fig. The magnitude and direction of the electric field is

1. 100 ${\mathrm{Vm}}^{-1}$ making angle 120$°$ with the x-axis
2. 200 ${\mathrm{Vm}}^{-1}$ making angle 60$°$ with the x-axis
3. 200 ${\mathrm{Vm}}^{-1}$ making angle 120$°$ with the x-axis
4. None of the above