Electric Charges & Fields

Two charges, each equal to $q,$ are kept at $x = - a$ and $x = a$ on the $x$ -axis. A particle of mass $m$ and charge $q_{0} = \frac{q}{2}$ $$ is placed at the origin. If charge $q_{0}$ $$ is given a small displacement $(y <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math> < < a)$ along the $y$ -axis, the net force acting on the particle is

1. $y$
2. $- y <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math>$
3. $1 / y <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math>$
4. $- 1 / y <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math>$

Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d(d<<l) apart because of their mutual repulsion. The change begins to leak from both the spheres at a constant rate. As a result the charges approach each other with a velocity v. Then as a function of distance x between them
1. $v \propto x^{- 1 / 2}$
2. $v \propto x^{- 1}$
3. $v \propto x^{1 / 2}$
4. $v \propto x$

Three infinitely long charge sheets are placed as shown in figure. The electric field at point $P$ is

1. $\frac{2 σ}{ε_{ο}} \hat{k}$
2. $−2σεοˆk<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mn>2</mn><mi>σ</mi></mrow><msub><mi>ε</mi><mi>ο</mi></msub></mfrac><mover><mi>k</mi><mo>^</mo></mover></math>$
3. $\frac{4 σ}{ε_{ο}} \hat{k}$
4. $−4σεοˆk<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mn>4</mn><mi>σ</mi></mrow><msub><mi>ε</mi><mi>ο</mi></msub></mfrac><mover><mi>k</mi><mo>^</mo></mover></math>$

Three concentric metallic spherical shells of radii $R, 2 R, 3 R$ , are given charges $Q 1 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mn>1</mn></msub></math>, Q 2 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mn>2</mn></msub></math>, Q 3 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mn>3</mn></msub></math> ,$ respectively. It is found that the surface charge densities on the outer surfaces of the shells are equal. Then, the ratio of the charges given to the shells, $Q 1 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mn>1</mn></msub></math>$ $ : Q 2 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mn>2</mn></msub></math> : Q 3 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mn>3</mn></msub></math> ,$ is

1. 1: 2: 3
2. 1: 3: 5
3. 1: 4: 9
4. 1: 8: 18

Consider a uniform spherical charge distribution of radius $R 1 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>R</mi><mn>1</mn></msub></math> $ centred at the origin O. In this distribution, a spherical cavity of radius $R 2 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>R</mi><mn>2</mn></msub></math>,$ centred at $P$ with distance $O P = a = R 1 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>R</mi><mn>1</mn></msub></math>$ $ -$ $R 2 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>R</mi><mn>2</mn></msub></math>$ (see figure) is made. If the electric field inside the cavity at position $\vec{r}$ is $\to E (\to r) <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mi>E</mi><mo>\to</mo></mover><mo>(</mo><mover><mi>r</mi><mo>\to</mo></mover><mo>)</mo></math>,$ then the correct statement(s) is(are)

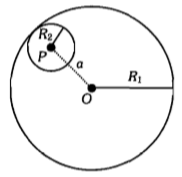
1. $\to E <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mi>E</mi><mo>\to</mo></mover></math>$ is uniform, its magnitude is independent of $R 2 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>R</mi><mn>2</mn></msub></math>$ $$ but its direction depends on $\vec{r}$

2. $\to E <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mi>E</mi><mo>\to</mo></mover></math>$ is uniform, its magnitude independs of $R 2 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>R</mi><mn>2</mn></msub></math>$ $$ and its direction depends on $\vec{r}$
3. $\to E <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mi>E</mi><mo>\to</mo></mover></math>$ is uniform, its magnitude is independent of a but its direction depends on $\vec{α}$
4. $\to E <math xmlns="http://www.w3.org/1998/Math/MathML"><mover><mi>E</mi><mo>\to</mo></mover></math>$ is uniform, and both its magnitude and direction depends on $\vec{α}$

Charge q is uniformly distributed over a thin half ring of radius $R .$ The electric field at the centre of the ring is

1. $q2π2ε0R2<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mi>q</mi><mrow><mn>2</mn><msup><mi>π</mi><mn>2</mn></msup><msub><mi>ε</mi><mn>0</mn></msub><msup><mi>R</mi><mn>2</mn></msup></mrow></mfrac></math>$
2. $q4π2ε0R2<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mi>q</mi><mrow><mn>4</mn><msup><mi>π</mi><mn>2</mn></msup><msub><mi>ε</mi><mn>0</mn></msub><msup><mi>R</mi><mn>2</mn></msup></mrow></mfrac></math>$ $$
3. $\frac{q}{4 π ε_{0} R^{2}}$
4. $\frac{q}{2 π ε_{0} R^{2}}$

Two concentric conducting thin spherical shells $A,$ and $B$ having radii $r A <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>r</mi><mi>A</mi></msub></math> $ and $r B <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>r</mi><mi>B</mi></msub></math> (r B <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>r</mi><mi>B</mi></msub></math> > r A <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>r</mi><mi>A</mi></msub></math> )$ are charged to $Q A <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mi>A</mi></msub></math> $ and $- Q B <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mi>B</mi></msub></math> (∣ Q B <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mi>B</mi></msub></math> ∣ > ∣ Q A <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>Q</mi><mi>A</mi></msub></math> ∣).$ The electrical field along a line, (passing through the centre) is

1.		2.
3.		4.

The spatial distribution of the electric field due to charges $(A, B)$ is shown in figure. Which one of the following statements is correct

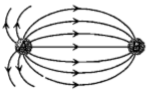
1. $A$ is $+$ ve and $B$ -ve and $∣ A ∣ > ∣ B ∣$
2. $A$ is -ve and $B + v e; ∣ A ∣ = ∣ B ∣$
3. Both are + ve but $A > B$
4. Both are -ve but $A > B$

Consider an electric field   $\vec{E} = E_{0} \hat{x}$ $,$ where $E_{0}$ is a constant. The flux through the bounded region (as shown in the figure) due to the field is -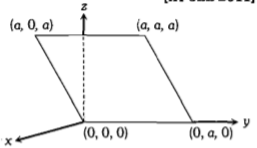
1.   $2 E_{0} α^{2}$
2.   $\sqrt{2} E_{0} α^{2}$
3.   $E_{0} α^{2}$
4.   $\frac{E_{0} α^{2}}{\sqrt{2}}$

10.

A charged ball $B$ hangs from a silk thread $S,$ which makes an angle $θ$ with a large charged conducting sheet $P$ as shown in the figure. The surface charge density of the sheet is proportional to

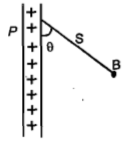
1. $cos θ$
2. $cot θ$
3. $sin θ$
4. $tan θ$

11.

Three charges $- q 1 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>q</mi><mn>1</mn></msub></math> + q 2 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>q</mi><mn>2</mn></msub></math> $ and $-$ $q_{3}$ s are placed as shown in the figure. The $x$ -component of the force on $- q 1 <math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>q</mi><mn>1</mn></msub></math> $ is proportional to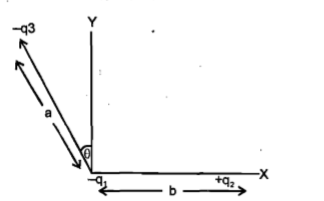

1. $q2b2-q3a2 <math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><msub><mi>q</mi><mn>2</mn></msub><msup><mi>b</mi><mn>2</mn></msup></mfrac><mo>-</mo><mfrac><msub><mi>q</mi><mn>3</mn></msub><msup><mi>a</mi><mn>2</mn></msup></mfrac><mo> </mo><mi>cos</mi><mi>θ</mi></math>$
$\frac{q_{2}}{b^{2}} + \frac{q_{3}}{a^{2}} \sin θ$
$\frac{q_{2}}{b^{2}} + \frac{q_{3}}{a^{2}} \cos θ$
$\frac{q_{2}}{b^{2}} - \frac{q_{3}}{a^{2}} \sin θ$

12.

Figure shows tracks of three charged particles in uniform electro static field. If $q_{1}$ $q_{2}$ and $q_{3}$ are the specific charges, that is charge per unit mass of the particles respectively, then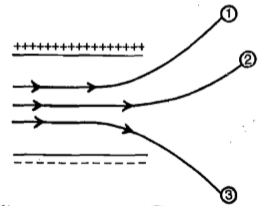

$q_{1}$ $q_{3}$
$q_{1}$
$q_{1}$
$q_{3}$

13.

Four particles, each having charge $q$ , are placed at four vertices of a regular pentagon. The distance of each comer from the centre is a . The electric field at the centre O of the pentagon is

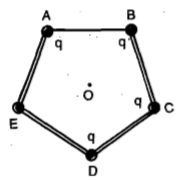
1. $\frac{q}{4 π ε_{0} a^{2}}$ along $E O$
2. $\frac{q}{2 π ε_{0} a^{2}}$ along $O E$
3. $\frac{q}{π ε_{0} a^{2}}$ along $E O$
4. $\frac{q}{4 π ε_{0} a^{2}}$

14.

The electric force between two short electric dipoles separated by a distance varies as:
1. $r^{2}$
2. $r^{4}$
3. $r^{- 2}$
4. $r^{- 4}$

15.

A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field E at the centre O is

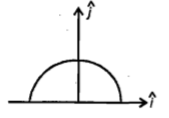
1. $\frac{q}{2 π^{2} ε_{0} r^{2}} \hat{j}$
2. $\frac{q}{4 π^{2} ε_{0} r^{2}} \hat{j}$
3. $- \frac{q}{4 π^{2} ε_{0} r^{2}} \hat{j}$
4. $- \frac{q}{2 π^{2} ε_{0} r^{2}} \hat{j}$

16. Let there be a spherically symmetric charge distribution with charge density varying as

$\rho(r)= \rho_0\left(\frac{5}{4}-\frac{r}{R}\right)$ upto

$r=R$ and

$\rho(r)= 0$ for

$r>R$ , where

$r$ is the distance from the origin. The electric field at a distance from the origin. The electric field at a distance

$r$ .

$(r>R)$ from the origin is given by:
1.

$\frac{\rho_{0} r}{3 \varepsilon_{0}} \left(\frac{5}{4} - \frac{r}{R}\right)$
2.

$\frac{4\pi\rho_{0} r}{3 \varepsilon_{0}} \left(\frac{5}{3} - \frac{r}{R}\right)$
3.

$\frac{\rho_{0} r}{3 \varepsilon_{0}} \left(\frac{5}{3} - \frac{r}{R}\right)$
4.

$\frac{4\rho_{0} r}{3 \varepsilon_{0}} \left(\frac{5}{4} - \frac{r}{R}\right)$

17.

A ring of charge with radius $0.5 m$ has 0.02 m gap. If the ring carries a charge of $+ 1 C,$ the field at the centre is

1. $^{4}$
2. $^{8}$
3. $^{4}$
4. $^{8}$

18.

Four charges equal to $- Q$ are placed at the four corners of a square and a charge $q$ is at its centre. If the system is in equilibrium the value of $q$ is
1. $- \frac{Q}{4} (1 + 2 \sqrt{2})$
2. $\frac{Q}{4} (1 + 2 \sqrt{2})$
3. $- \frac{Q}{2} (1 + 2 \sqrt{2})$
4. $\frac{Q}{2} (1 + 2 \sqrt{2})$

19.

Point charge $q$ moves from point $P$ to point $S$ along the path $PQRS$ (figure) in a uniform electric field $E$ pointing parallel to the positive direction of the $x\text-$ axis. The coordinates of the points $P,Q, R$ and $S$ are $(a, b, 0), (2a, 0, 0), (a, -b,0)$ and $(0, 0, 0)$ respectively. The work done by the field in the above process is given by expression: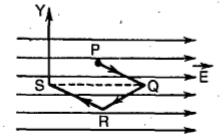

1. $qEa$
2. $-qEa$
3. $-qEa\sqrt{2}$
4. $qE\sqrt{2a^2+b^2}$

20.

A metallic sphere is placed in a uniform electric field. The lines of force follow the path
(s) shown in the figure as

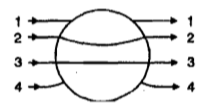
1. 1
2. 2
3. 3
4. 4

Fill OMR Sheet*

*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there

CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course

Please be patient as the PDF generation may take upto a minute.

Fill OMR Sheet*