Three masses are placed on the x-axis: \(300\) g at the origin, \(500\) g at \(x =40\) cm, and \(400\) g at \(x=70\) cm. The distance of the center of mass from the origin is:
1. \(40\) cm
2. \(45\) cm
3. \(50\) cm
4. \(30\) cm
A uniform square plate \(ABCD\) has a mass of \(10\) kg.
If two point masses of \(5\) kg each are placed at the corners \(C\) and \(D\) as shown in the adjoining figure, then the centre of mass shifts to the mid-point of:

1. \(OH\)
2. \(DH\)
3. \(OG\)
4. \(OF\)
1. \(\left(-\frac{15}{7}, \frac{85}{17}, \frac{1}{7}\right) \text{cm}\)
2. \(\left(\frac{15}{7},-\frac{85}{17}, \frac{1}{7}\right) \text{cm}\)
3. \(\left(\frac{15}{7}, \frac{85}{21},-\frac{1}{7}\right)\text{cm}\)
4. \(\left(\frac{15}{7}, \frac{85}{21}, \frac{7}{3}\right)\text{cm}\)
The centre of the mass of \(3\) particles, \(10~\text{kg},\) \(20~\text{kg},\) and \(30~\text{kg},\) is at \((0,0,0).\) Where should a particle with a mass of \(40~\text{kg}\) be placed so that its combined centre of mass is \((3,3,3)?\)
1. \((0,0,0)\)
2. \((7.5, 7.5, 7.5)\)
3. \((1,2,3)\)
4. \((4,4,4)\)
Two particles of mass, \(2\) kg and \(4\) kg, are projected from the top of a tower simultaneously, such that \(2\) kg of mass is projected with a speed \(20\) m/s at an angle \(30^{\circ}\) above horizontal and \(4\) kg is projected at \(40\) m/s horizontally. The acceleration of the centre of mass of the system of two particles will be:
1. \(\dfrac{g}{2}\)
2. \(\dfrac{g}{4}\)
3. \(g\)
4. \(2g\)
Five uniform circular plates, each of diameter \(D\) and mass \(m,\) are laid out in a pattern shown. Using the origin shown, the \(y\text-\text{coordinate}\) of the centre of mass of the ''five–plate'' system will be:

| 1. | \(\frac{2D}{5}\) | 2. | \(\frac{4D}{5}\) |
| 3. | \(\frac{D}{3}\) | 4. | \(\frac{D}{5}\) |
| 1. | \(9.9~\text m\) | 2. | \(10.1~\text m\) |
| 3. | \(10~\text m\) | 4. | \(20~\text m\) |
At \(t=0,\) the positions of the two blocks are shown. There is no external force acting on the system. Find the coordinates of the centre of mass of the system (in SI units) at \(t=3\) seconds.

| 1. | \((1,0)\) | 2. | \((3,0)\) |
| 3. | \((4.5,0)\) | 4. | \((2.25,0)\) |
A bomb is projected from the ground at a horizontal range of \(R\). If the bomb explodes mid-air, then the range of its centre of mass is:
1. \(\frac{R}{2}\)
2. \(R\)
3. \(2R\)
4. \(\frac{2R}{3}\)
Three identical spheres, each of mass \(M\), are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to \(2~\text{m}\) (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the centre of mass.
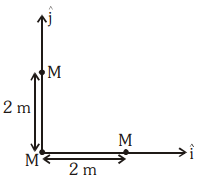
| 1. | \(2( \hat{i}+ \hat{j})\) | 2. | \(( \hat{i}+ \hat{j})\) |
| 3. | \({2 \over 3}( \hat{i}+ \hat{j})\) | 4. | \({4 \over 3}( \hat{i}+ \hat{j})\) |






