A pendulum oscillates about its mean position \(\mathrm{C}.\) The position where the speed of the bob becomes maximum is: (ignore all dissipative forces)

1.
\(\mathrm{A}\)
2.
\(\mathrm{B}\)
3.
\(\mathrm{C}\)
4.
\(\mathrm{D}\)

| 1. | \(T_1<T_2\) | 2. | \(T_1>T_2\) |
| 3. | \(T_1=T_2\) |
4. | \(T_1= 2T_2\) |
The position x (in centimeter) of a simple harmonic oscillator varies with time t (in second) as . The magnitude of the maximum acceleration of the particle in is:
1. /2
2. /4
3. /2
4. /4
A horizontal platform is executing simple harmonic motion in the vertical direction with frequency f. A block of mass m is placed on the platform. What is the maximum amplitude of the SHM, so that the block is not detached from it?
1.
2.
2.
4.
A body at the end of a spring executes S.H.M. with a period while the corresponding period for another spring is . If the period of oscillation with two springs in series is T, then:
1.
2.
3.
4.
A body is executing linear S.H.M. At a position x, its potential energy is , and at a position y, its potential energy is . The potential energy at the position (x + y) is
1.
2.
3.
4.
The equation of a particle executing simple harmonic motion is (where t is in seconds and y is in meters). The initial phase of the particle is:
1.
2.
3.
4.
An ideal spring-mass system has a time period of vibration T. If the spring is cut into 4 identical parts and same mass oscillates with one of these parts, then the new time period of vibration will be
1.
2. T
3.
4. 2T
The equation of a particle executing simple harmonic motion is Displacement y from the mean position where acceleration becomes zero is: (y is in cm and t is in second)
1. 2 cm
2. 0
3. cm
4. cm
The displacement \((\mathrm{x})\) of an SHM varies with time \((\mathrm{t})\) as shown in the figure. The frequency of variation of potential energy is:
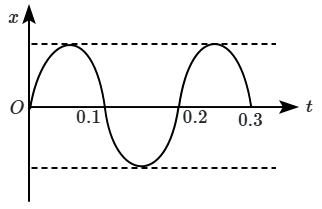
1. \(5\text{ Hz}\)
2. \(10\text{ Hz}\)
3. \(40\text{ Hz}\)
4. \(20\text{ Hz}\)






